Las técnicas de inteligencia artificial existen desde hace varias décadas, y no se limitan solamente al aprendizaje de máquina, las redes neuronales, la lógica difusa o el aprendizaje profundo.  Existe una técnica que permite modelar estados temporales de sistemas altamente complejos y que es capaz de predecir los cambios de estos sistemas mediante la aplicación de reglas simples de evolución. Dicha técnica de la inteligencia artificial se conoce como el paradigma de los Autómatas Celulares. 

Los Autómatas Celulares (AC) son pequeños elementos que ocupan espacios o celdas unitarias dentro de un dominio discreto bidimensional o tridimensional denominado malla o red, cuyo volumen representa el sistema modelado (Figura 1). Cada autómata localizado en una celda de esta malla posee un estado, dentro de un grupo de estados predefinidos, que a través de la interacción entre sí y con sus celdas vecinas puede mantenerse o cambiar a través de las iteraciones de evolución del sistema modelado, esto gracias a que cada autómata tiene la capacidad de tomar decisiones de forma independiente para mantener o cambiar dicho estado mientras el sistema evoluciona. Al proyectar este comportamiento del autómata a una escala mayor, se logra modelar sistemas altamente complejos cuyo comportamiento macro es gobernado por el comportamiento de sus unidades componentes más pequeñas.

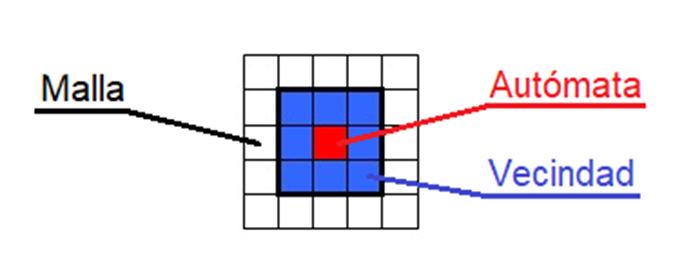
La evolución del estado del autómata se basa en la aplicación de reglas individuales de evolución muy simples. En cada iteración, el autómata conoce únicamente su propio estado y el estado de sus vecinos más próximos, y en función de estos estados y de las reglas de evolución, el autómata evoluciona a la siguiente iteración manteniendo o cambiando su estado.     

Las celdas que contienen los autómatas, y que a su vez conforman la malla o dominio del sistema modelado, pueden ser cuadradas, triangulares o poligonales en el caso bidimensional o bien hexaédricas o tetraédricas en el dominio tridimensional.  

Para conocer el estado de sus vecinos, el autómata utiliza un tipo de vecindad para relacionarse con su entorno, el cual depende del número de autómatas vecinos que se tengan en cuenta. Las vecindades utilizadas van desde la vecindad vacía, el la cual el autómata solo se tiene en cuenta a sí mismo, hasta las vecindades que toman en cuenta a cuatro (von Neumann), ocho (Moore), doce (von Neumann expandida, MvonN) o veinticuatro (Moore expandida) vecinos. Esta última incluye los autómatas vecinos a primer y a segundo nivel de distancia (Figura 2, fila superior).  

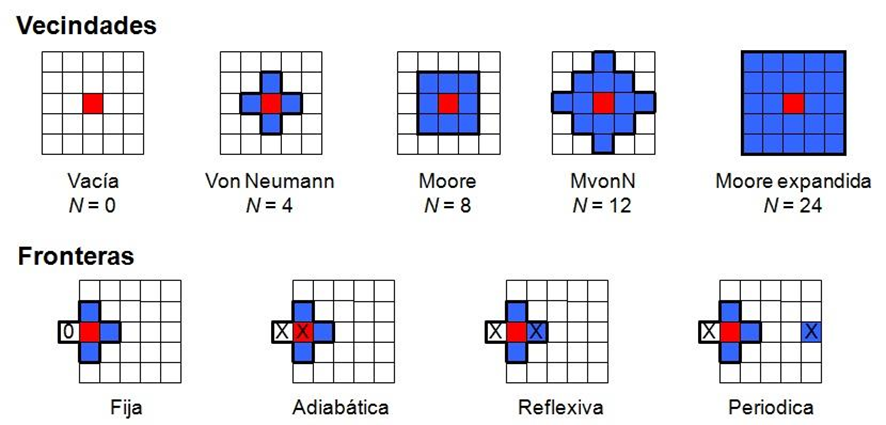
Cuando el autómata se encuentra en una frontera del dominio, también toma en cuenta diversas configuraciones para las hipotéticas celdas vecinas ubicadas fuera de la frontera, que les asignan estados específicos para la iteración y la evolucion. Dentro de las configuraciones para estas posiciones fuera del dominio se les puede asignar un estado nulo (frontera fija), el mismo estado del autómata en la frontera (frontera adiabática), el mismo estado que tiene el autómata ubicado al lado contralateral de la frontera (frontera reflexiva) o el estado que tiene el autómata ubicado en la misma fila y al extremo opuesto de la malla (frontera periódica), (Figura 2, fila inferior).   

El paradigma de los autómatas celulares apareció en la decada de 1940 por Stanislaw Ulam para describir gráficamente el crecimiento de cristales. Simultáneamente, Von Neumann utilizó la misma herramienta para estudiar sistemas capaces de autoreproducirse. En los 70´s John Conway utiliza el concepto de los AC para crear el juego de la vida, un modelo con capacidad dinámica de los autómatas para desplazarse y replicarse por la implementación de unas reglas simples de evolución (Figura 3, A). En 1983, Wolfram presenta en su obra a new kind of science el desarrollo de diversas reglas que generan series de formas regulares e irregulares que se autoreplican (Figura 3, B). En 1993, Ermentrout et al. utilizan por primera vez los AC en la generación de redes biológicas como el sistema neuronal y el sistema circulatorio, tomando el modelo como un proceso continuo (Figura 3, C). Para 2004, Deutch et al. desarrollan los primeros modelos de crecimiento de tumores (Figura 3, D).

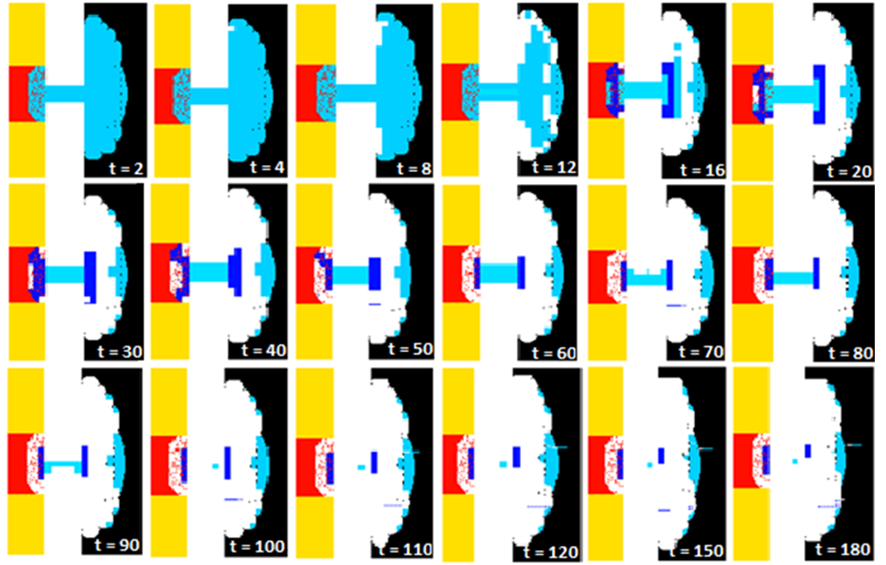
Hasta la fecha los autómatas celulares han sido utilizados para simular y predecir comportamientos en diversos sistemas tales como la formación de fractales, el comportamiento de poblaciones bacterianas, el análisis del trafico en las grandes ciudades, la creación de estructuras por optimización topológica, e incluso la arquitectura de los tejidos y el tiempo de curación en un proceso de reparación de fractura ósea (Figura 4). 

En resumen, los autómatas celulares, una destacada técnica de la inteligencia artificial, permiten analizar y predecir el comportamiento de diversos sistemas altamente complejos de una manera simple y sencilla.

Referencias

[1] A.J. Arias-Moreno. “Modelo computacional para la simulación del proceso de osteogénesis y curación ósea después de la fractura”. Tesis de maestría, Universidad Nacional de Colombia, Colombia, enero de 2011.

[2] A. Tovar. “Bone remodeling as a hybrid cellular automaton optimization process”. Tesis doctoral, University of Notre Dame, Estados Unidos, diciembre de 2004. 

Otros posts