Profesor a Tiempo Completo
Dpto. de Bioingeniería e Ing. Química
Andrei Markov fue un matemático ruso que trabajo y contribuyo a la teoría de los procesos estocásticos. Las cadenas de Markov describen un proceso aleatorio en el que el estado futuro del sistema depende únicamente de su estado presente y no de su historia pasada. Las cadenas de Markov tienen numerosas aplicaciones en campos como la física, la biología, la química, la economía, la informática, la ingenieria, etc.
Las cadenas de Markov proporcionan un marco poderoso para modelar sistemas biológicos estocásticos y tiene aplicaciones en la Genética, la Bioinformática, la Epidemiología, la Neurociencia. Por ejemplo:
- En genética de poblaciones, las cadenas de Markov se usan para modelar el desvío genético que ocurre cuando las poblaciones experimentan fluctuaciones aleatorias en las frecuencias alélicas;
- En bioinformática, se utilizan para alinear secuencias múltiples e identificar patrones de regiones conservadas en secuencias de ADN o proteínas;
- En Epidemiología: los modelos de Markov se pueden usar para modelar la propagación de enfermedades infecciosas donde se construye modelos de susceptible-infectado-recuperado (SIR) que tiene estados donde las personas se mueven entre: susceptible, infectado y recuperado.
- En Neurociencia: las cadenas de Markov se usan para modelar los patrones de activación de las neuronas en respuesta a estímulos o los patrones de conectividad de las redes neuronales.
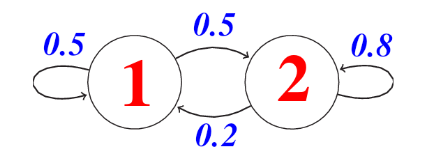
Las cadenas de Markov son modelos gráficos probabilísticos que representan un proceso dinámico que cambia con el tiempo. Para que cualquier proceso sea considerado para el modelado con la Cadena de Markov, debe asumir la Propiedad de Markov que establece que el estado siguiente (t+1) solo depende del estado actual (t) y es independiente de todos los estados anteriores desde (t-1, t-2, …), es decir, para conocer un estado futuro, solo necesitamos conocer el estado actual.
Entonces podemos ver una cadena de Markov (MC) como una máquina de estados discretos con transiciones no deterministas entre estados, es decir, existe una probabilidad de transitar de un estado “p” a otro estado “k”. Formalmente, una cadena de Markov de n estados y que tiene S0 como estado inicial se especifica con los siguientes tres elementos:
- Conjunto de estados: Q = {S1, S2, . . . , Sn}
- Probabilidades de ocurrencia de cada estado: Π = {π1, π2, . . . , πn}, donde πk = P(S0 = qk)
- Probabilidades de cambio de estado de uno a otro: P(St = K | St−1 = p )

Un modelo de cadena de Markov puede ayudar a responder básicamente tres tipos de preguntas:
- ¿Cuál es la probabilidad de una determinada secuencia de estados?
- ¿Cuál es la probabilidad de que la cadena permanezca en cierto estado por un período de tiempo?
- ¿Cuál es el tiempo esperado que la cadena permanecerá en un estado determinado?
La estimación de parámetros de una cadena de Markov sigue siendo un desafío. Para algunos modelos, los parámetros se pueden estimar simplemente contando el número de veces que la secuencia está en un cierto estado, p, y el número de veces que hay una transición de un estado p a un estado k. Si tenemos N secuencias de observaciones. λ0p es el número de veces que el estado p es el estado inicial de una secuencia, λp es el número de veces que observamos el estado p y λpk es el número de veces que observamos una transición del estado p al estado k. Las probabilidades iniciales serian πp = λ0p/N y las probabilidades de transición serian apk = λpk/λp
Se usan cadenas ocultas de Markov (HMM) cuando los estado no se pueden observar directamente, sino solo el resultado de alguna función de probabilidad de los estados. HMM es un modelo estadístico en el que se supone que el sistema que se modela es un proceso de Markov con estados no observados (ocultos). Un modelo de Markov es útil cuando necesitamos calcular una probabilidad para una secuencia de eventos observables. Sin embargo, en muchos casos los eventos que nos interesan no se observan directamente. Un HMM nos permite hablar sobre eventos observados y eventos ocultos que consideramos como factores causales en nuestro modelo probabilístico.
Un ejemplo seria el problema de reconocimiento del sitio de empalme 5′ de un ADN (Fig 3). Si nos dan una secuencia de ADN que comienza en un exón, contiene un sitio de empalme 5′ y termina en un intrón. El problema es identificar dónde ocurrió el cambio de exón a intrón, dónde está el sitio de empalme 5′ (5′SS). Si los exones tienen una composición de base uniforme en promedio (25%), los intrones son ricos en A/T (40% cada uno para A/T, 10% cada uno para C/G) y el nucleótido de consenso 5’SS es casi siempre una G (95% G y 5% A).
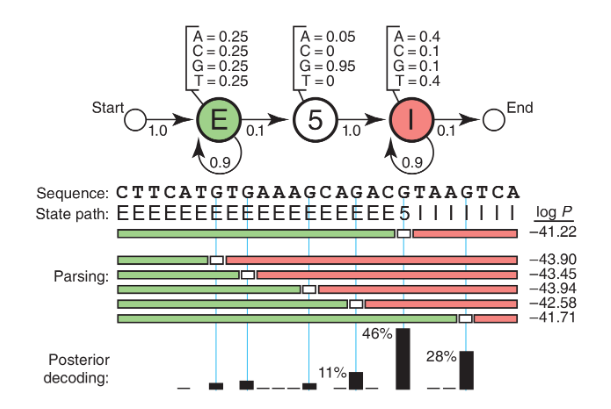
Con esta información se podemos dibujar un HMM (Fig. 3) que tiene tres estados, uno para cada una de las tres etiquetas que podríamos asignar a un nucleótido: E (exón), 5 (5′SS) e I (intrón). Cada estado tiene sus propias probabilidades de emisión, que modelan la composición base de exones, intrones y el consenso G en el 5′SS. Cada estado también tiene probabilidades de transición (flechas), las probabilidades de pasar de este estado a un nuevo estado. El modelo genera dos cadenas de información si al visitar un estado, se emite un residuo de la distribución de probabilidad de emisión del estado y despues se va otro estado de acuerdo con la distribución de probabilidad de transición del estado. El primero representa la ruta de estado (etiquetas) a medida que hacemos la transición de un estado a otro y el segundo representa la secuencia observada (ADN). La ruta de estado es una cadena de Markov debido a que el siguiente estado depende solo del estado presente. Dado que solo se da la secuencia observada, esta ruta de estado está oculta y son las etiquetas de residuos usados. El camino del estado es una cadena de Markov oculta. Finalmente, la probabilidad P(S,π|HMM,θ) de que un HMM con parámetros θ genere un camino de estado π y una secuencia observada S es el producto de todas las probabilidades de emisión y de transición que se utilizaron.
A pesar que el problema de estimar una distribución discreta desconocida a partir de sus muestras fue un problema complejo y durante la última década se hizo un esfuerzo de investigación significativo que lo resolvió para una variedad de medidas de divergencia. Sin embargo, construir y estimar una cadena de Markov desconocida y sus parámetros a partir de sus muestras es aun un problema muy complejo.
Actualmente profesores de Bioingeniería de UTEC se encuentran trabajando en proyectos relacionados a las cadenas de Markov con aplicaciones biológicas. Si estás interesado en ser parte de los proyectos que esperas: ¡Únete a Bioingeniería de la UTEC!
Referencias:
- Caswell, H 2001 Matrix Population Models. 2nd Ed. Sinauer Assoc. Inc., Sunderland, MA
- Grassly NC, Fraser C. Mathematical models of infectious disease transmission. Nat Rev Microbiol. 2008;6(6):477–487.
- Balzter H . Markov chain models for vegetation dynamics. Ecological Modelling. 2000;126(2–3):139–154.
- Choo KH, Tong JC, Zhang L. Recent applications of Hidden Markov Models in computational biology. Genomics Proteomics Bioinformatics. 2004;2(2):84–96.
- Koski T. Hidden markov models for bioinformatics. Springer Netherlands; 2001.
- Eddy, S. What is a hidden Markov model?. Nat Biotechnol 22, 1315–1316 (2004). https://doi.org/10.1038/nbt1004-1315
- Grewal, J.K., Krzywinski, M. & Altman, N. Markov models—Markov chains. Nat Methods 16, 663–664 (2019). https://doi.org/10.1038/s41592-019-0476-x
- Djordjevic IB. Markov Chain-Like Quantum Biological Modeling of Mutations, Aging, and Evolution. Life (Basel). 2015 Aug 24;5(3):1518-38. doi: 10.3390/life5031518. PMID: 26305258; PMCID: PMC4598651.
- Athey, T.L., Tward, D.J., Mueller, U. et al. Hidden Markov modeling for maximum probability neuron reconstruction. Commun Biol 5, 388 (2022). https://doi.org/10.1038/s42003-022-03320-0
- Chen, Y., Baños, R. & Buceta, J. A Markovian Approach towards Bacterial Size Control and Homeostasis in Anomalous Growth Processes. Sci Rep 8, 9612 (2018). https://doi.org/10.1038/s41598-018-27748-9
- Armond, J., Saha, K., Rana, A. et al. A stochastic model dissects cell states in biological transition processes. Sci Rep 4, 3692 (2014). https://doi.org/10.1038/srep03692
- Barra, M., Dahl, F.A., Vetvik, K.G. et al. A Markov chain method for counting and modelling migraine attacks. Sci Rep 10, 3631 (2020). https://doi.org/10.1038/s41598-020-60505-5